ImperialViolet

In an upcoming paper (made public this morning), Nadhem AlFardan and Kenny Paterson describe another method of performing Vaudenay's attack on CBC as used in TLS. Firstly I'd like to thank the researchers for notifying the various vendors ahead of time so that patches could be prepared: the disclosure process has gone very smoothly in this case. I couldn't have asked for anything more - they did everything right.

Vaudenay's attack requires an attacker to be able to detect when a CBC padding check has succeeded, even if the authentication check then fails. Authentication should always be applied after encryption to avoid this, but TLS famously did it the wrong way round with CBC mode.

Knowing whether a padding check succeeded reveals information about the decrypted plaintext. By tweaking the ciphertext over many trials, it's possible to progressively decrypt an unknown ciphertext. For details, see their paper, which does a better job of explaining it than I would.

Vaudenay first used the fact that these two situations (padding check failure and authenticator failure) resulted in different TLS alert values, although that didn't result in a practical attack because TLS errors are encrypted. Once that was corrected (by specifying that the same alert value should be sent in each case) the next year's paper used a timing-side channel: if the authentication check wasn't performed when the padding check failed then, by timing the server's response, an attacker could tell whether the server aborted processing early.

To try and remove that side-channel, TLS stacks perform the authentication check whether or not the padding check succeeds. However, here's what I commented in the Go TLS code:

Note that we still have a timing side-channel in the MAC check, below. An attacker can align the record so that a correct padding will cause one less hash block to be calculated. Then they can iteratively decrypt a record by breaking each byte. However, our behavior matches OpenSSL, so we leak only as much as they do.

That pretty much sums up the new attack: the side-channel defenses that were hoped to be sufficient were found not to be (again). So the answer, this time I believe, is to make the processing rigorously constant-time. (Details below.)

As a practical matter, since a padding or authenticator check failure is fatal to a TLS connection, performing this attack requires a client to send the same plaintext secret on thousands of different connections to the same server. This isn't a trivial obstacle but it's possible to meet this requirement for cookies with a browser and bit of Javascript injected into any origin in the same session.

For DTLS the attack is much easier because a rejected record doesn't cause the connection to be destroyed and the same authors developed a method for amplifing timing attacks against DTLS in a previous paper

Unfortunately, unlike BEAST, this isn't something that we can unilaterally fix on the client side (except by disabling CBC mode, which might have significant compatibility issues.) On the server side, making RC4 the most preferable cipher solves the problem although I do recommend that server admins apply patches as they become available even so. Having RC4 as an option has been a useful fallback for CBC problems but, if patches aren't applied, then RC4 becomes a monoculture in the future.

Implementing constant time CBC decoding

Fixing this problem in a backwards compatible manner is, sadly, really rather complex. What need to ensure that all CBC records are authenticated in constant time. Initially we define constant-time to mean that, for all values of the secret input, the trace of instructions executed and memory locations accessed is identical (on an in-order machine). Here the secret input is the decrypted CBC record before the padding and MAC have been checked.

Meeting this definition is tough and there's a great temptation to remove some of the more glaring timing leaks and hope that the remainder is small enough not to be practical. But the DTLS trick mentioned above can be used to amplify any timing side-channels. Additionally, situations change and implementations that are currently only exposed over a network may, in the future, be exposed to attackers running on the same machine. At that point, cache-line probing and other powerful timing probes can be brought to bear against any side-channels that remain.

For the purposes of this post, we consider the decrypted, CBC record to contain the following parts:

1. n bytes of plaintext. (Which may be compressed but, within our scope, it's plaintext.)
2. mac_size bytes of MAC. (Up to 48 bytes in TLS with SHA-384. We conservatively assume that the minimum number of MAC bytes is zero since this is clearly a valid lower-bound and accounts for truncated MAC extensions.)
3. padding_length bytes of padding.
4. One byte of padding length. (Some consider this to be part of the padding itself, but I'll try to be consistent that this length byte is separate.)

With this secret data in hand, we need to perform three steps in constant time:

1. Verify that the padding bytes are correct: the padding cannot be longer than the record and, with SSLv3, must be minimal. In TLS, the padding bytes must all have the same value as the length byte.
2. Calculate the MAC of the header and plaintext (where the header is what I'm calling the additional data that is also covered by the MAC: the sequence number etc).
3. Extract the MAC from the record (with constant memory accesses!) and compare it against the calculated MAC.

Utilities

We will make extensive use of bitwise operations and mask variables: variables where the bits are either all one or all zero. In order to create mask values it's very useful to have a method of replicating the most-significant-bit to all the bits in a value. We'll assume that an arithmetic right shift will shift in the MSB and perform this operation for us:

#define DUPLICATE_MSB_TO_ALL(x) ( (unsigned)( (int)(x) >> (sizeof(int)*8-1) ) )
#define DUPLICATE_MSB_TO_ALL_8(x) ( (uint8_t)( (int8_t)(x) >> 7) )

However, note that the C standard does not guarantee this behaviour, although all CPUs that I've encountered do so. If you're worried then you can implement this as a series of logical shifts and ORs.

We'll define some more utility functions as we need them.

SSLv3 padding

SSLv3 padding checks are reasonably simple: we need only to test that the padding isn't longer than the record and that it's less than a whole cipher block. We assume that the record is at least a byte long. (Note that the length of the whole record is public information and so we can fast reject invalid records if we're using that length alone.) We can use the fact that, if a and b are bounded such that the MSB cannot be set, then the MSB of a - b is one iff b>a.

padding_length = data[length-1];
unsigned t = (length-1)-padding_length;
unsigned good = DUPLICATE_MSB_TO_ALL(~t);
t = block_size - (padding_length+1);
good &= DUPLICATE_MSB_TO_ALL(~t);

The resulting value of good is a mask value which is all ones iff the padding is valid.

TLS padding

Padding in TLS differs in two respects: the value of the padding bytes is defined and must be checked, and the padding is not required to be minimal. Therefore we must always make memory accesses as if the padding was the maximum length, with an exception only in the case that the record is shorter than the maximum. (Again, the total record length is public information so we don't leak anything by using it.)

Here we use a mask variable (mask), which is all ones for those bytes which should be part of the padding, to discard the result of checking the other bytes. However, our memory access pattern is the same for all padding lengths.

unsigned padding_length = data[length-1];
unsigned good = (length-1)-padding_length;
good = DUPLICATE_MSB_TO_ALL(~good);
unsigned to_check = 255; /* maximum amount of padding. */
if (to_check > length-1) {
        to_check = length-1;
}

for (unsigned i = 0; i < to_check; i++) {
        unsigned t = padding_length - i;
        uint8_t mask = DUPLICATE_MSB_TO_ALL(~t);
        uint8_t b = data[length-1-i];
        good &= ~(mask&(padding_length ^ b));
}

If any of the padding bytes had an incorrect value, or the padding length was invalid itself, one of more of the bottom eight bits of good will be zero. Now we can map any value of good with such a zero bit to 0, and leave the case of all ones the same:

good &= good >> 4;
good &= good >> 2;
good &= good >> 1;
good <<= sizeof(good)*8-1;
good = DUPLICATE_MSB_TO_ALL(good);

In a very similar way, good can be updated to check that there are enough bytes for a MAC once the padding has been removed and then be used as a mask to subtract the given amount of padding from the length of the record. Otherwise, in subsequent sections, the code can end up under-running the record's buffer.

Calculating the MAC

All the hash functions that we're concerned with are Merkle–Damgård hashes and nearly all used in TLS have a 64-byte block size (MD5, SHA1, SHA-256). Some review of this family of hash functions is called for:

All these hash functions have an initial state, a transform function that takes exactly 64 bytes of data and updates that state, and a final_raw function that marshals the internal state as a series of bytes. In order to hash a message, it must be a multiple of 64 bytes long and that's achieved by padding. (This is a completely different padding than discussed above!)

In order to pad a message for hashing, a 0x80 byte is appended, followed by the minimum number of zero bytes needed to make the length of the message congruent to 56 mod 64. Then the length of the message (not including the padding) is written as a 64-bit, big-endian number to round out the 64 bytes. If the length of the message is 0 or ≥ 55 mod 64 then the padding will cause an extra block to be processed.

In TLS, the number of hash blocks needed to compute a message can vary by up to six, depending on the length of the padding and MAC. Thus we can process all but the last six blocks normally because the (secret) padding length cannot affect them. However, the last six blocks need to be handled carefully.

The high-level idea is that we generate the contents of each of the final hash blocks in constant time and hash each of them. For each block we serialize the hash and copy it with a mask so that only the correct hash value is copied out, but the amount of computation is constant.

SHA-384 is the odd one out: it has a 128 byte block size and the serialised length is twice as long, although it is otherwise similar. The example below assumes a 64 byte block size for clarity.

We calculate two indexes: index_a and index_b. index_a is the hash block where the application data ends and the 0x80 byte is put. index_b is the final hash block where the length bytes are put. They may be the same, or index_b may be one greater. We also calculate c: the offset of the 0x80 byte in the index_a block.

The arithmetic takes some thought. One wrinkle so far ignored is that additional data is hashed in prior to the application data. TLS uses HMAC, which includes a block containing the masked key and then there are 13 bytes of sequence number, record type etc. SSLv3 has more than a block's worth of padding data, MAC key, sequence etc. These are collectively called the header here. The variable k in the following tracks the starting position of the data for the constant time blocks and includes this header.

for (i = num_starting_blocks; i <= num_starting_blocks+varience_blocks; i++) {
        uint8_t block[64];
        uint8_t is_block_a = constant_time_eq(i, index_a);
        uint8_t is_block_b = constant_time_eq(i, index_b);
        for (j = 0; j < 64; j++) {
                uint8_t b = 0;
                if (k < header_length) {
                        b = header[k];
                } else if (k < data_plus_mac_plus_padding_size + header_length) {
                        b = data[k-header_length];
                }
                k++;

                uint8_t is_past_c = is_block_a & constant_time_ge(j, c);
                uint8_t is_past_cp1 = is_block_a & constant_time_ge(j, c+1);
                /* If this is the block containing the end of the
                 * application data, and we are at, or past, the offset
                 * for the 0x80 value, then overwrite b with 0x80. */
                b = (b&~is_past_c) | (0x80&is_past_c);
                /* If this the the block containing the end of the
                 * application data and we're past the 0x80 value then
                 * just write zero. */
                b = b&~is_past_cp1;
                /* If this is index_b (the final block), but not
                 * index_a (the end of the data), then the 64-bit
                 * length didn't fit into index_a and we're having to
                 * add an extra block of zeros. */
                b &= ~is_block_b | is_block_a;

                /* The final eight bytes of one of the blocks contains the length. */
                if (j >= 56) {
                        /* If this is index_b, write a length byte. */
                        b = (b&~is_block_b) | (is_block_b&length_bytes[j-56]);
                }
                block[j] = b;
        }

        md_transform(md_state, block);
        md_final_raw(md_state, block);
        /* If this is index_b, copy the hash value to |mac_out|. */
        for (j = 0; j < md_size; j++) {
                mac_out[j] |= block[j]&is_block_b;
        }
}

Finally, the hash value needs to be used to finish up either the HMAC or SSLv3 computations. Since this involves processing an amount of data that depends only on the MAC length, and the MAC length is public, this can be done in the standard manner.

In the case of SSLv3, since the padding has to be minimal, only the last couple of hash blocks can vary and so need to be processed in constant time. Another optimisation is to reduce the number of hash blocks processed in constant time if the (public) record length is small enough that some cannot exist for any padding value.

The above code is a problem to implement because it uses a different hash API than the one usually provided. It needs a final_raw function that doesn't append the hash padding, rather than the common final function, which does. Because of this implementers may be tempted to bodge this part of the code and perhaps the resulting timing side-channel will be too small to exploit, even with more accurate local attacks. Or perhaps it'll be good for another paper!

Extracting the MAC from the record.

We can't just copy the MAC from the record because its position depends on the (secret) amount of padding. The obvious, constant-time method of copying out the MAC is rather slow so my thanks to Emilia Kasper and Bodo Möller for suggesting better ways of doing it.

We can read every location where the MAC might be found and copy to a MAC-sized buffer. However, the MAC may be byte-wise rotated by this copy so we need to do another mac_size² operations to rotate it in constant-time (since the amount of rotation is also secret):

unsigned mac_end = length;
unsigned mac_start = mac_end - md_size;
/* scan_start contains the number of bytes that we can ignore because the
 * MAC's position can only vary by 255 bytes. */
unsigned scan_start = 0;
if (public_length_inc_padding > md_size + 255 + 1) {
        scan_start = public_length_inc_padding - (md_size + 255 + 1);
}
unsigned char rotate_offset = (mac_start - scan_start) % md_size;

memset(rotated_mac, 0, sizeof(rotated_mac));
for (unsigned i = scan_start; i < public_length_inc_padding; i += md_size) {
        for (unsigned j = 0; j < md_size; j++) {
                unsigned char mac_started = constant_time_ge(i + j, mac_start);
                unsigned char mac_ended = constant_time_ge(i + j, mac_end);
                unsigned char b = 0;
                if (i + j < public_length_inc_padding) {
                        b = data[i + j];
                }
                rotated_mac[j] |= b & mac_started & ~mac_ended;
        }
}

/* Now rotate the MAC */
memset(out, 0, md_size);
for (unsigned i = 0; i < md_size; i++) {
        unsigned char offset = (md_size - rotate_offset + i) % md_size;
        for (j = 0; j < md_size; j++) {
                out[j] |= rotated_mac[i] & constant_time_eq_8(j, offset);
        }
}

Finally, the MAC should be compared in constant time by ORing a value with the XOR of each byte in place from the calculated and given MACs. If the result is zero, then the record is valid. In order to avoid leaking timing information, the mask value from the padding check at the very beginning should be carried throughout the process and ANDed with the final value from the MAC compare.

Limitations of our model

We started out by defining constant-time with a specific model. But this model fails in a couple of ways:

Firstly, extracting the MAC as detailed above is rather expensive. On some chips all memory accesses within a cache-line are constant time and so we can relax our model a little and use a line-aligned buffer to perform the rotation in when we detect that we're building on such a platform.

Secondly, when I sent an early version of the OpenSSL patch to the paper's authors for them to test, they reported that they found a timing difference! I instrumented the OpenSSL code with the CPU cycle counter and measured a median time of 18020 cycles to reject a record with a large amount of padding but only 18004 cycles with small padding.

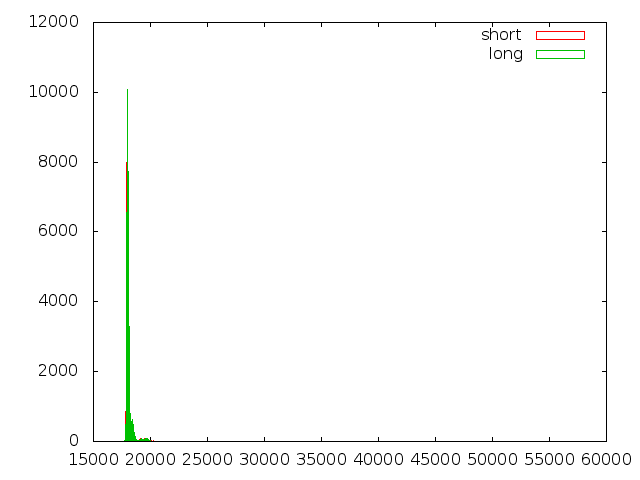
This difference may be small, but it was stable. To cut a long story short, it came from this line:

unsigned char rotate_offset = (mac_start - scan_start) % md_size;

When the padding was larger, the MAC started earlier in the record (because the total size was the same). So the argument to the DIV instruction was smaller and DIV, on Intel, takes a variable amount of time depending on its arguments!

The solution was to add a large multiple of md_size to make the DIV always take the full amount of time (and to do it in such a way that the compiler, hopefully, won't be able to optimise it away). Certainly 20 CPU cycles is probably too small to exploit, but since we've already “solved” this problem twice, I'd rather not have to worry in the future.